11.13 Beugung an Gittern
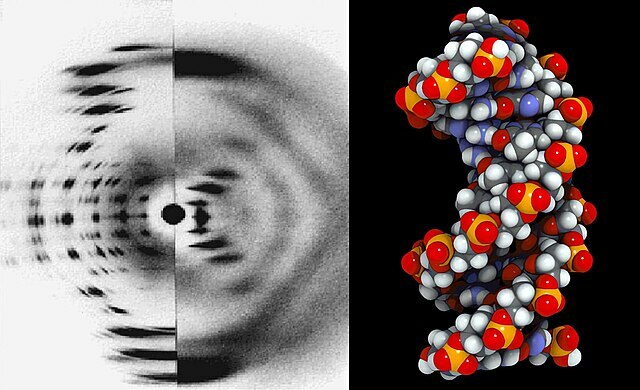
In Bild 11.135 siehst du links eines der Fotos mit deren Hilfe es 1952 gelang die Doppel-Helix Struktur des DNA-Strangs (rechts) zu entdecken. Ihre Entschlüsselung gilt als eine der größten Leistungen in der Geschichte der Wissenschaft (Nobelpreis für Medizin 1962).
Bisher sind wir von sich geradlinig ausbreitenden Lichtstrahlen ausgegangen (geometrische Optik). Licht hat aber Welleneigenschaften. In diesem und den nächsten Kapiteln wirst du Experimente kennenlernen, bei denen der Wellencharakter von Licht eindeutig zu Tage tritt und die Näherung der geometrischen Optik nicht mehr gilt. Der Fachbereich der Wellenoptik (engl. physical optics oder wave optics) befasst sich mit den Welleneigenschaften von Licht. In diesen Kapiteln wirst du erfahren, welche Lichterscheinungen an feinen Strukturen zu beobachten sind und eine Idee davon bekommen, wie es Mitte des 20. Jahrhunderts möglich war, das DNA Molekül zu entschlüsseln.
11.13.1 Doppelspalt-Experiment mit Licht
Richten wir einen grünen Laserpointer (Lichtwellenlänge: \(532\;\mathrm{nm}\)) auf eine Blende mit zwei Schlitzen (Doppelspalt), deren Spaltbreite in der Größenordnung der Lichtwellenlänge liegt, erhalten wir das Muster aus Bild 11.136 an der Wand dahinter.
Das Muster kennen wir bereits von Wasserwellen. Wie bei dem Doppelspalt-Experiment mit Wasserwellen, wird in jedem der beiden Blendenöffnungen je eine kreisförmige Elementarwelle angeregt. Diese beiden Elementarwellen überlagern sich und bilden das Interferenzmuster an der Wand (Bild 11.137).
Der Zusammenhang zwischen der Wellenlänge des Lichts und den Abständen der Stellen maximaler Helligkeit findest du im Abschnitt über den Versuchsaufbau des Doppelspalt-Experiments von Thomas Young.
11.13.2 Gangunterschied für konstruktive Interferenz
Konstruktive Interferenz (Verstärkung) entsteht, wenn sich die Wellen aus beiden Spalten gleichphasig überlagern (Bild 11.138).
Damit ein Wellenberg auf einen Wellenberg trifft darf es entweder keinen Gangunterschied geben oder der Gangunterschied \(\Delta s\) muss ein ganzzahliges Vielfaches der Wellenlänge \(\lambda\) betragen. Die Bedingung für konstruktive Interferenz lautet daher:
\[ \Delta s = 0, \pm\lambda, \pm2\cdot\lambda, \pm3\cdot\lambda, \ldots \]
Oder allgemein:
\[ \boxed{\Delta s = \pm n\cdot\lambda, \qquad n=0,1,2,3,\ldots} \]
11.13.3 Gangunterschied für destruktive Interferenz
Destruktive Interferenz (Auslöschung) entsteht, wenn sich die Wellen aus beiden Spalten gegenphasig überlagern (Bild 11.139).
Damit ein Wellenberg auf ein Wellental trifft, muss der Gangunterschied \(\Delta s\) entweder eine halbe Wellenlänge oder ein ganzzahliges Vielfaches plus einer halben Wellenlänge \(\lambda\) betragen. Die Bedingung für destruktive Interferenz lautet daher:
\[ \Delta s = \pm\frac{1}{2}\cdot\lambda, \pm(1+\frac{1}{2})\cdot\lambda, \pm(2+\frac{1}{2})\cdot\lambda, \ldots \]
Oder allgemein:
\[ \boxed{\Delta s = \pm (n+\frac{1}{2})\cdot\lambda, \qquad n=0,1,2,3,\ldots} \]
In manchen Texten findest du die mit der Gleichung oben gleichwertige Darstellung („ungerades Vielfaches der halben Wellenlänge“):
\[ \Delta s = \pm \frac{2\cdot n+1}{2}\cdot\lambda \]
11.13.4 Kohärentes Licht
Das Doppelspalt-Experiment ist mit Laserlicht heute sehr einfach durchzuführen. Das liegt daran, dass Laserlicht ganz besondere Eigenschaften hat. Zum einen sendet ein Laser monochromatisches Licht (engl. monochromatic light) aus (Licht einer einzigen Wellenlänge). Das ist keine Selbstverständlichkeit. Weißes Licht von der Sonne enthält zum Beispiel alle Wellenlängen. Um ein Interferenzmuster beobachten zu können, müssen die Lichtwellen außerdem kohärent (engl. coherent), daher eine zeitlich fixe Phasenbeziehung haben. Das Bezeichnung leitet sich von dem lateinischen Wort cohaerere für „zusammenhängen“ ab.
In Bild 11.140 (a) siehst du weißes Licht wie es von der Sonne kommt. Die Überlagerung all dieser Wellenzüge ändert sich ständig. In (b) siehst du monochromatisches Licht. Die Wellenzüge sind aber nicht in „Reih und Glied“, daher ändert sich die Überlagerung ständig. In (c) siehst du schließlich monochromatisches und kohärentes Licht. Die Amplitude ändert sich mit der Zeit nicht.
Die meisten Lichtquellen liefern weder monochromatisches (Ausnahme: Natriumdampflampe mit einer Wellenlänge von \(590\;\mathrm{nm}\)) noch kohärentes Licht. Mithilfe eines Glasprismas im Strahlengang lassen sich die Lichtfarben (und damit die Wellenlägen) jedoch trennen. Fällt das Licht dahinter auf eine Blende mit einem schmalen Spalt in der Größenordnung der Lichtwellenlänge, wird an der Öffnung nahezu kohärentes Licht angeregt. Auf diese Weise erhalten wir monochromatisches und kohärentes Licht mit einer beliebigen Lichtquelle.
11.13.6 Intensitätsverteilung beim Doppelspalt
Immer wenn wir eine komplizierte zeitliche oder örtliche Beziehung zwischen zwei winkelabhängigen Vektorgrößen haben, können wir auf ein Zeigerdiagramm zurückgreifen.
In Bild 11.141 siehst du das Zeigerdiagramm für das Doppelspalt-Experiment. Die Wellenamplituden der beiden Spalte werden mit zwei Zeigern \(z_1\) und \(z_2\) dargestellt. Der Winkel zwischen beiden Zeigern entspricht dem Gangunterschied an dem jeweiligen Punkt an der Wand. Die Gesamtamplitude ergibt sich aus der Vektorsumme beider Zeiger (\(z_\text{ges}\)). Zeigen beide in dieselbe Richtung, herrscht konstruktive Interferenz. Sind beide Zeiger entgegen gerichtet löschen sie sich aus und wir haben den Fall destruktiver Interferenz. Für alle anderen Gangunterschiede erhalten wir einen Wert zwischen diesen beiden Extremen. Die wahrgenommene Lichthelligkeit (Intensität) ist durch die Kreisfläche um die Zeiger angedeutet. Sie ist proportional der zweiten Potenz der Gesamtamplitude. Die Intensitätsverteilung ändert sich mit \(I(\alpha) \propto \cos(\alpha)^2\).
11.13.7 Interferenzmuster bei n-Spaltöffnungen
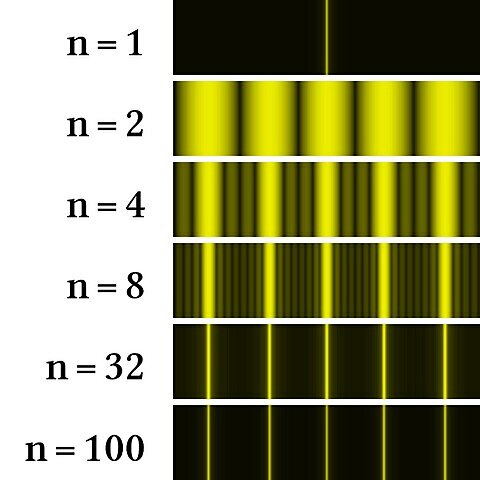
Lassen wir die Anordnung des Doppelspalt-Versuchs unverändert, aber erhöhen die Anzahl der Spaltöffnungen (wobei der Spaltabstand unverändert bleibt!) erhalten wir die Interferenzmuster in Bild 11.142.
Für einen Spalt (\(n=1\)) erhalten wir kein Interferenzmuster, für \(n=2\) das aus dem Doppelspalt-Versuch bekannte Muster. Erhöhen wir die Spaltanzahl können wir erkennen, dass die Hauptmaxima immer dünner und intensiver werden. Außerdem bilden sich zwischen den Hauptmaxima noch Nebenmaxima (Maxima mit geringer Helligkeit) heraus. Bei sehr großer Spaltzahlen (\(n=100\)) erhalten wir schließlich sehr scharfe Beugungsbilder, während im Bereich dazwischen (fast) überall vollständige Auslöschung durch destruktive Interferenz stattfindet.
11.13.8 Intensitätsverteilung Spaltgitter
Um zu verstehen, wieso es bei einer größeren Anzahl an Spaltöffnungen zu den Nebenmaxima kommt und warum die Hauptmaxima immer schärfer werden, verwenden wir wieder die Zeigerdarstellung der Amplituden, die uns schon bei der Intensitätsverteilung beim Doppelspalt gute Dienste geleistet hat.
In Bild 11.143 siehst du das Interferenzmuster, das bei drei Spaltöffnungen entsteht. Beim Hauptmaximum zeigen alle drei Pfeile in dieselbe Richtung und wir haben maximale Verstärkung (1). Ändern wir den Winkel kommt es zu einem Gangunterschied der Wellenzüge. Die Gesamtamplitude sinkt (2). Bilden die drei Pfeile schließlich ein gleichseitiges Dreieck, ist die Gesamtamplitude null (3). Das Zeigerpolygon faltet sich immer weiter zusammen (4), bis es in (5) maximal gefaltet ist. An dieser Stelle erhalten wir ein Nebenmaximum. Die Amplitude ist hier ein Drittel der Amplitude des Hauptmaximums (ein neuntel der Maximalintensität). Ab jetzt beginnt sich die Zeiger wieder aufzufalten. Nach einem weiteren Minimum in (6) entfaltet sich das Zeigerpolygon wieder zu voller Größe und bildet das Hauptmaximum 1-Ordnung. Startest du das App hinter dem Bild kannst du die Zeigerpolygone für die Spaltanzahl zwei bis zehn selbst erforschen.
Bild 11.144: Vergleich Intensitätsverteilung bei \(n\) Spaltöffnungen (Höhen der Maxima nicht im richtigen Verhältnis)
In Bild 11.144 siehst du die Intensitätsverteilung bei einer noch höheren Zahl an Spaltöffnungen. Zwischen zwei Hauptmaxima liegen immer \(N − 1\) Minima und \(N − 2\) Nebenmaxima. Mit zunehmender Spaltanzahl \(N\) werden die Nebenmaxima zwar immer zahlreicher, aber auch schwächer. Die Gesamtenergie verteilt zunehmen auf die Hauptmaxima, die dadurch „schärfer“ werden. Der Verlauf der Intensität kann durch folgende Formel angenähert werden (ohne Herleitung):
\[ I(\alpha) \propto \frac{\cos(N\cdot x)-1}{\cos(x)-1} \]
11.13.9 Interferenz bei Gittern
Verwenden wir statt einer Spaltblende ein regelmäßiges Strichgitter, erhalten wir ein zweidimensionales Interferenzmuster. Das Muster in Bild 11.145 wurde mit einer weißen LED und einem Strichgitter aus \(34{.}290\) Linien pro Zentimeter in horizontaler und vertikaler Richtung erzeugt.
Wir können beobachten, dass die roten Anteile des Lichts stärker abgelenkt werden als die blauen. Nach Gleichung (A.5) folgt daraus, dass rötliches Licht eine größere Wellenlänge hat als bläuliches Licht.
Durch die vielen Linien des Gitters sind die Maxima sehr scharf und die Messung ihrer Abstände wird entsprechend genau.
Die Symmetrieeigenschaften des Gitters finden sich in den Symmetrieeigenschaften des Beugungsbildes wieder. Mit der Formel (A.5) können wir bei bekannter Wellenlänge auf die Gitterkonstante (Abstände im Gitter) schließen.
11.13.10 Kristallstrukturanalyse
Da sich Wellen bei kleinen Hindernissen gleich wie bei kleinen Öffnungen verhalten, liefern sie ein identisches Beugungsbild. Die Atome im regelmäßigen Gitter eines Kristalls verhalten sich daher ähnlich den Öffnungen in einem optischen Gitter (Bild 11.146).
Während sichtbares Licht eine Wellenlänge von rund \(5\cdot10^{-7}\;\mathrm{m}\) besitzt, bewegen sich die Abstände der Atome in einem Kristall in der Größenordnung von \(3\cdot10^{-10}\;\mathrm{m}\). Für ein brauchbares Beugungsbild ist die Wellenlänge also rund 1000 Mal zu groß. „Licht“ mit der passenden Wellenlänge liegt im Röntgenbereich. Für die Kristallstrukturanalyse (engl. x-ray crystallography) werden daher monochromatische Röntgenstrahlen verwendet. Als Beispiel findest du am Kapitelanfang das Beugungsbild eines DNA-Stranges, das die Struktur der Doppel-Helix wiedergibt (Bild 11.135).
Links:
- Artikel (englisch): Photo 51
11.13.11 Holografie
In Bild 11.147 siehst du ein Hologramm aus zwei unterschiedlichen Betrachtungswinkeln. Anders als bei einem Foto kannst du bei einem Hologramm eine Szene räumlich wie durch ein Fenster betrachten.
Die Idee, das Interferenzmuster von Licht für die räumliche Rekonstruktion einer Szene zu verwenden, stammt von Dennis Gábor (Nobelpreis für Physik 1971). Von ihm stammt auch der Name Holografie (engl. holography). Er leitet sich von den griechischen Wörtern ὅλος (holos, bedeutet „ganz“, „vollständig“) und γραφία (graphia, bedeutet „aufgezeichnet“) ab. In Bild 11.148 siehst du das Prinzip, wie ein Hologramm aufgezeichnet wird. Das monochromatische und kohärente Licht eines Lasers wird durch einen Strahlenteiler in einen Objektstrahl und einen Referenzstrahl aufgeteilt. Der Objektstrahl trifft in der Folge auf das Objekt und streut das Licht in Richtung Film. Über einen Spiegel trifft auch der Referenzstrahl auf den Film. Die beiden Strahlen überlagern sich und bilden ein Interferenzmuster, das am Hologramm festgehalten wird (Bild 11.148).
Für die Wiederherstellung des Interferenzmusters wird ein Laser mit denselben Eigenschaften im gleichen Winkel wie bei der Aufnahme auf den Film gerichtet. Die Wellenfront wird an der Filmschicht so gebeugt, dass wir als Betrachter die ursprüngliche Intensitätsverteilung in Abhängigkeit vom Betrachtungswinkel sehen (Bild 11.149).
Schneidest du die Hälfte von einem Foto weg, kannst du nur die Bildinformation auf der übrigen Hälfte sehen. Die Bildinformation ist ja nur an einer einzigen Stelle am Foto gespeichert. Bei einem Hologramm ist das anders. Schneidest du die Hälfte von einem Hologramm weg, siehst du immer noch das ganze Bild! In einem Hologramm ist an jeder Stelle die Information von jedem Objektpunkt zu einem Teil enthalten. Durch das Entfernen eines Teils des Hologramms wird nur die Bildqualität schlechter.
Neben der Kunst werden Hologramme auch für die Langzeitspeicherung von Daten verwendet. Weil Hologramme aufwendig herzustellen sind, findest du sie als zusätzliches Sicherheitsmerkmal manchmal auf Kredit- und Bankkarten.
Ein Linsenrasterbild („Wackelkarte“, engl. lenticular printing), wie du es manchmal auf Postkarten oder Lesezeichen findest, ist kein Hologramm. Bei dieser Technik werden dir abhängig vom Betrachtungswinkel eine fixe Anzahl von Bildern gezeigt, die Bewegung oder Räumlichkeit vortäuschen.