14.13 Ideale Kreisprozesse und Wirkungsgrad
In Bild 14.85 siehst du eine abgefeuerte Kugel aus einem Revolver.
Das entspricht thermodynamisch einer adiabatischen Expansion, bei der – wenn wir Reibung vernachlässigen – die entstehende Wärme vollständig in Bewegungsenergie umgewandelt wird. Allerdings handelt es sich dabei um eine einmalige Umwandlung von Wärme in mechanische Arbeit. In der Praxis sind vor allem Prozesse von Bedeutung, bei denen es zu einer wiederholten Umwandlung von Wärme in mechanische Arbeit kommt. Um diese Prozesse geht es in diesem Kapitel. Zunächst werden wir uns mit dem Begriff des Kreisprozesses näher beschäftigen und uns dann der Frage nach dem maximalen Wirkungsgrad von Maschinen widmen.
14.13.1 Kreisprozess
In Bild 14.86 siehst du die adiabatische Expansion eines Gases im p-V-Diagramm, zum Beispiel für die abgefeuerte Kugel aus der Kapitel-Einleitung (Kurvenstück 1). Die Fläche unter der Kurve entspricht der vom Gas verrichteten Arbeit (Beschleunigungsenergie) an der Kugel.
Stellen wir uns stattdessen einen Kolben in einem gasgefüllten Zylinder vor, der adiabatisch expandiert. Um eine wiederholte Umwandlung von Wärme in mechanische Arbeit zu erhalten, muss die Expansion unterbrochen werden und der Kolben durch weitere thermodynamische Prozesse wieder in den ursprünglichen Zustand übergeführt werden. In unserem Beispieldiagramm 14.86 sind das eine isobare Kompression (Kurvenstück 2) und eine isochore Erwärmung (Kurvenstück 3). Jetzt kann der Zyklus erneut beginnen. Um den Kreislauf zu schließen, muss immer Arbeit von außen aufgebracht werden! Im Bild entspricht diese Arbeit der schraffierten Fläche.
Ein Kreisprozess ist eine Kombination aus unterschiedlichen Zustandsänderungen, die eine Arbeitssubstanz (üblicherweise ein Gas) periodisch wieder in den ursprünglichen Zustand zurückversetzen. Diese Schritte werden bei Motoren auch „Takte“ genannt, um anzudeuten, dass sie sich in regelmäßigen Abständen wiederholen.
Viele Kreisprozesse bestehen aus einer Kombination von vier paarweise verschiedenen thermodynamischen Prozessen, zum Beispiel aus zwei isothermen und zwei isochoren Zustandsänderungen (Stirling-Kreisprozess) oder zwei isothermen und zwei adiabatischen Zustandsänderungen (Carnot-Kreisprozess).
Je nachdem in welcher Richtung ein Kreisprozess im p-V-Diagramm durchlaufen wird, handelt es sich um eine Wärmekraftmaschine (Uhrzeigersinn) oder eine Wärmepumpe/Kältemaschine (Gegenuhrzeigersinn).
14.13.2 Energiefluss bei einem Kreisprozess
Um den Ausgangszustand im p-V-Diagramm wieder zu erreichen, muss immer ein Teil der zugeführten Wärme für die Rückführung des Prozesses aufgewendet werden. Dieser Teil der Wärmeenergie steht nicht zur Umwandlung in mechanische Energie zur Verfügung und wird als abgeführte Wärme bezeichnet.
| Bei einer kontinuierlichen oder zyklischen Umwandlung von Wärme in Arbeit muss immer auch Wärme im Laufe des Kreisprozesses abgeführt werden. |
Der Energiefluss einer Wärmekraftmaschine (engl. heat engine) ist in Bild 14.87 zusammengefasst.
Die Maschine entnimmt der Wärmequelle die Wärmemenge \(Q_H\) und gibt einen Teil dieser Wärme \(Q_K\) an eine Wärmesenke (Umgebung) ab. Die Differenz \(Q_H-Q_K\) ist die nutzbare mechanische Arbeit \(W\). Die Bezeichnungen „Quelle“ und „Senke“ für die beiden Wärmebereiche sind ein Hinweis darauf, in welche Richtung die Wärme von selbst fließen würde.
In Bild 14.88 siehst du den Energiefluss einer umgekehrt arbeitenden Wärmekraftmaschine – einer Wärmepumpe (engl. heat pump).
Die Maschine entnimmt der Wärmesenke mithilfe der mechanischen Arbeit \(W\) die Wärme \(Q_K\) und gibt sie als Wärme \(Q_H\) an die Wärmequelle ab. Hier muss also (in den meisten Fällen mechanische) Energie zugeführt werden, damit Wärme vom kälteren zum heißeren Medium fließen kann.
14.13.3 Thermischer Wirkungsgrad
Der thermische Wirkungsgrad \(\eta\) (engl. thermal efficiency) einer Wärmekraftmaschine ist eine dimensionslose Größe (Verhältniszahl), die angibt, wie effizient Wärme in Arbeit umgesetzt wird. Das Formelsymbol für den Wirkungsgrad ist der griechische Kleinbuchstabe Eta.
Eine Maschine ist umso effizienter, je weniger Wärme \(Q_H\) wir der Wärmequelle entnehmen müssen und je größer die gewonnene nutzbare Arbeit \(W\) ist. Der thermische Wirkungsgrad ist daher definiert als:
| \[\begin{equation} \eta = \frac{\text{nutzbare Arbeit}}{\text{aufzuwendende Wärmemenge}} = \frac{W}{Q_{H}} \tag{14.25} \end{equation}\] |
Zum Beispiel bedeutet ein thermischer Wirkungsgrad \(\eta = 0.6\), dass aus 10 Teilen thermischer Energie 6 Teile mechanischer Energie gewonnen werden können und 4 Teile der thermischen Energie gehen als Abwärme verloren (Bild 14.89).
Bild 14.89: Beispiel eines thermischen Wirkungsgrads einer Wärmekraftmaschine (grüne Quadrate entsprechen Energieeinheiten)
Da nie die gesamte Wärme in Arbeit umgewandelt werden kann, muss der Wirkungsgrad immer kleiner als eins sein (\(0\le \eta < 1\)). Aus idealen Kreisprozessen (Stirling-Kreisprozess, Carnot-Kreisprozess,…) wurde abgeleitet, dass der maximal mögliche thermische Wirkungsgrad einer Wärmekraftmaschine nur von den Temperaturen der Wärmequelle \(T_H\) und der Wärmesenke \(T_K\) abhängt. Er ist:
\[\begin{equation} \eta_{max} = 1 - \frac{T_{K}}{T_{H}} \tag{14.26} \end{equation}\]
Der maximal mögliche Wirkungsgrad ist unabhängig von dem jeweils gewählten Kreisprozess und ist für alle zwischen denselben Temperaturen arbeitenden reversiblen Kreisprozessen gleich groß!
Durch Verluste (Reibung,…) wird der reale Wirkungsgrad in Bezug auf den theoretisch maximal möglichen Wirkungsgrad zusätzlich verkleinert.
\[ \eta_{real} < \eta_{max} \]
Ein 4-Takt-Ottomotor hat eine Arbeitstemperatur von rund \(T_H=2600\;\mathrm{K}\) und eine Abgastemperatur von rund \(T_K=970\;\mathrm{K}\). Aus diesen beiden Temperaturen ergibt sich ein maximaler Wirkungsgrad von \(\eta_{max, Otto} = 0{,}62\ldots\), also ein Wert weit unter 1! Reibung und andere Verluste schränken den Wirkungsgrad von realen Ottomotoren weiter ein. Im optimalen Fall wird in der Praxis ein Wirkungsgrad von rund \(\eta_{real, Otto} = 0{,}5\) erreicht – etwa die Hälfte der Energie geht an Abwärme verloren. Der reale Wirkungsgrad von Wärmekraftmaschinen liegt bei rund \(20\,\%-40\,\%\).
Für umgekehrt arbeitende Wärmekraftmaschinen wird die Effizienz je nach Anwendung durch die Leistungszahl einer Wärmepumpe oder die Leistungszahl einer Kältemaschine angegeben.
14.13.4 Reversible und irreversible Prozesse
Bei reversiblen Prozessen (engl. reversible process) kann ein thermodynamisches System nach einer Zustandsänderung auf demselben Weg im p-V-Diagramm in seinen ursprünglichen Zustand zurückgeführt werden. Dabei befindet sich das System die ganze Zeit über in einem Gleichgewichtszustand (Im gesamten System gibt es zu jedem Zeitpunkt keine Druck-, Temperatur- oder Dichteunterschiede). Alle anderen Prozesse werden irreversibel (engl. irreversible process) genannt.
Ein reversibler Prozess ist eine theoretische Idealisierung. Alle bekannten natürlichen Prozesse sind irreversibel, weil Reibung, Wirbelbildung und andere sogenannte dissipativen Effekte unvermeidlich sind. Reversible Prozesse sind deshalb aber nicht unsinnig. Sie helfen uns zu verstehen, was thermodynamische Maschinen im besten Fall leisten können.
Obwohl Prozesse in der Natur immer irreversibel sind, sind einige fast reversibel. Dafür muss jede Änderung
- sehr langsam und
- in sehr kleinen Schritten
erfolgen. Damit hat das Medium (zum Beispiel ein Gas) genügend Zeit, etwaige Druck-, Temperatur- oder Dichteunterschiede verschiedener Bereiche auszugleichen. Solche Änderungen werden auch quasistatisch (engl. quasi static) genannt.
Als Beispiel sieh dir das System in Bild 14.90 an.
Wir komprimieren ein Gas sehr langsam, indem wir Sandkörner auf den (fast) reibungsfreien Kolben rieseln lassen. Durch den thermischen Kontakt des Gases zu einem großen Wärmebecken unter dem Zylinder wird jeder Temperaturanstieg im Gas als Wärme an das Becken abgegeben. Wir erhalten also eine (fast) reversible isotherme Kompression. Die Größen Druck, Temperatur und Volumen sind zu allen Zeiten des Prozesses wohldefinierte Werte – das Gas befindet sich zu jedem Zeitpunkt (fast) in einem Gleichgewichtszustand.
Da es sich um einen reversiblen Prozess handelt, können wir das Gas auf demselben Weg wieder expandieren. Dazu entfernen wir Sandkorn für Sandkorn wieder von dem Kolben. Jede Temperatursenkung wird durch eine Wärmezufuhr aus dem Wärmebecken ausgeglichen und wir erreichen eine (fast) reversible isotherme Expansion.
14.13.5 Stirling-Kreisprozess
Ein idealer reversibler Kreisprozess ist der Stirling-Kreisprozess (engl. stirling cycle), benannt nach Robert Stirling.
Er besteht aus folgenden 4 Takten (Bild 14.91):
1. Takt: Reversible isotherme Expansion: Die Expansion von Volumen \(V_A\) auf \(V_B\) erfolgt mit konstanter Temperatur \(T_H\) in einem heißen Wärmebecken. Da sich die Innere Energie bei einem isothermen Prozess nicht ändert, wird die aus dem heißeren Wärmebecken aufgenommene Wärme \(Q_1\) direkt als Arbeit \(W_1\) an dem Kolben verrichtet.
\[ Q_1 = W_1 \]
2. Takt: Reversible isochore Abkühlung: Die Temperatur des Gases wird von der Temperatur \(T_H\) auf \(T_K\) abgesenkt. Das geschieht, indem der Zylinder samt Kolben (genügend langsam) in das kalte Wärmebecken gebracht wird. Dabei wird die Position des Kolbens im Zylinder nicht verändert – in diesem Takt wird also keine Arbeit verrichtet (\(W_2=0\)). Das Wärmebecken nimmt dabei die Wärmemenge \(Q_2\) auf, wodurch die Innere Energie des Gases um \(\Delta U_2\) sinkt.
\[ \Delta U_2 = Q_2 \]
Dabei sinkt natürlich der Druck von \(p_B\) auf \(p_C\).
3. Takt: Reversible isotherme Kompression: Die Kompression von Volumen \(V_C\) auf \(V_D\) erfolgt bei konstanter Temperatur \(T_K\). Da sich die Innere Energie bei einem isothermen Prozess nicht verändert, wird die aufgebrachte Arbeit \(W_3\) direkt an das kältere Wärmebecken in Form von Wärme \(Q_3\) abgegeben.
\[ Q_3 = W_3 \]
4. Takt: Reversible isochore Abkühlung: Die Temperatur des Gases wird von der Temperatur \(T_K\) auf \(T_H\) angehoben. Das geschieht, indem der Zylinder samt Kolben (genügend langsam) in das Wärmebecken der höheren Temperatur gebracht wird. Dabei wird die Position des Kolbens im Zylinder nicht verändert – in diesem Takt wird also keine Arbeit verrichtet (\(W_4=0\)). Das Wärmebecken gibt dabei die Wärmemenge \(Q_4\) ab, wodurch die Innere Energie des Gases um \(\Delta U_4\) steigt.
\[ \Delta U_4 = Q_4 \]
Zusätzlich zur Temperatur steigt der Druck von \(p_D\) auf \(p_A\). Das Gas befindet sich jetzt im selben thermischen Zustand (A) wie zu Beginn des 1. Takts und kann einen weiteren Zyklus durchlaufen.
14.13.6 Wirkungsgrad Stirling-Kreisprozess
Wir werden jetzt eine Formel für den Wirkungsgrad des Stirling-Kreisprozess herleiten.
Im ersten Takt (isotherme Expansion) wird dem Gas die Wärme \(Q_1\) aus dem heißeren Wärmebecken zugeführt und dabei restlos als Arbeit genutzt (\(W_1=Q_1\) und \(\Delta U=0\)).
Im dritten Takt (isotherme Kompression) muss die gesamte verrichtete Arbeit \(W_3\) in Form von Wärme \(Q_3\) in das Wärmebecken mit der tieferen Temperatur abgeführt werden (\(W_3=Q_3\) und \(\Delta U=0\)).
Sowohl im zweiten als auch im vierten Takt wird überhaupt keine Arbeit verrichtet (isochore Prozesse). Die im Takt zwei abgeführte Wärme \(Q_2\) und die im Takt vier aufgenommene Wärme \(Q_4\) sind betragsmäßig gleich groß und heben daher einander auf.
Der Wirkungsgrad einer Wärmekraftmaschine ist definiert als:
\[ \eta = \frac{\text{nutzbare Arbeit}}{\text{aufzuwendende Wärmemenge}} \]
Für den Stirling-Kreisprozess bedeutet das konkret:
\[ \eta = \frac{W_1-W_3}{Q_1} = \frac{Q_1-Q_3}{Q_1} = 1-\frac{Q_3}{Q_1} \]
Wählen wir ein bestimmtes Volumen \(V_x\), dann gilt für den Druck \(p_o\) auf der oberen Isotherme (Temperatur \(T_H\)) nach dem idealen Gasgesetz:
\[ p_o=n\cdot k\cdot \frac{T_H}{V_x} \]
Und für den Druck \(p_u\) auf der unteren Isotherme (Temperatur \(T_K\)):
\[ p_u=n\cdot k\cdot \frac{T_K}{V_x} \]
Für das Verhältnis der Drücke erhältst du:
\[ \frac{p_u}{p_o} = \frac{n\cdot k\cdot \frac{T_K}{V_x}}{n\cdot k\cdot \frac{T_H}{V_x}} = \frac{T_K}{T_H} \]
Die Arbeit \(W_1\) und \(W_3\), die als Flächeninhalte unter den Isothermen im p-V-Diagramm zu sehen sind, können wir durch Rechtecke beliebig genau annähern (Bild 14.92). Sehen wir uns zunächst das Verhältnis der Teilarbeiten \(\Delta W_3\) und \(\Delta W_1\) (Flächeninhalte zweier rechteckförmigen Streifen) an einer beliebigen Stelle in unserer Annäherung an:
\[ \frac{\Delta W_3}{\Delta W_1} = \frac{p_u\cdot\Delta V}{p_o\cdot\Delta V} = \frac{p_u}{p_o} = \frac{T_K}{T_H} \]
Das Verhältnis der Teilarbeiten ist also nur von dem Temperaturverhältnis abhängig. Da wir keine bestimmte Stelle gewählt haben, gilt dasselbe Verhältnis nicht nur für alle Streifen, sondern auch für das Verhältnis der Summen über alle Streifen und damit sogar für das Verhältnis der Gesamtarbeiten:
\[ \frac{W_3}{W_1} = \frac{T_K}{T_H} \]
Für den Stirling-Prozess gilt \(W_3 = Q_3\) und \(W_1 = Q_1\) und du erhältst damit für den Wirkungsgrad einer idealen Stirling Wärmekraftmaschine \(\eta_s\) die Formel:
\[ \eta_s = 1-\frac{Q_3}{Q_1}= 1-\frac{W_3}{W_1}= 1-\frac{T_K}{T_H} \]
Bei dem reversiblen Stirling-Kreisprozess hängt der Wirkungsgrad nur von der Temperaturdifferenz von beiden Wärmebehältern ab.
Da der ideale Stirling-Kreisprozess reversibel ist, kann er in umgekehrter Richtung als Wärmepumpe verwendet werden. Die Leistungszahl \(\epsilon_{\text{s}}\) eines umgekehrt ablaufenden Stirling-Kreisprozesses lautet daher:
\[ \epsilon_{\text{s}} = \frac{1}{\eta_{c}} = \frac{T_{H}}{T_{H}-T_{K}} \]
14.13.7 Stirlingmotor
Im Gegensatz zum Carnot Kreisprozess gibt es Wärmekraftmaschinen, die nach dem Prinzip des Stirling-Kreisprozesses arbeiten. In Bild 14.93 siehst du einen Stirlingmotor, der nur durch die Temperaturdifferenz von Hautoberfläche und Umgebungstemperatur läuft.
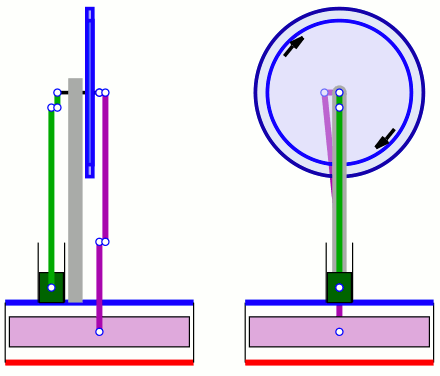
In Bild 14.94 siehst du die Funktionsweise des Stirlingmotors. Ein Gas wird von außen in einem abgeschlossenen Raum erhitzt (zum Beispiel von der Handwärme) und es expandiert. In einem anderen abgeschlossenen Raum wird es gekühlt (zum Beispiel von der Umgebung) und es komprimiert. Das Gas pendelt zwischen diesen beiden Räumen und wechselt dabei Temperatur und Druck.
Stirlingmotoren können bei sehr geringen Temperaturunterschieden noch arbeiten, haben aber insgesamt einen sehr geringen Wirkungsgrad und werden in der Praxis wenig verwendet.
Links:
14.13.8 Carnot Kreisprozess
Ein anderer idealer reversibler Kreisprozess ist der Carnot Kreisprozess (engl. carnot cycle), benannt nach Nicolas Léonard Sadi Carnot.
Er besteht aus folgenden 4 Takten (Bild 14.95):
1. Takt: Reversible isotherme Expansion: Die Expansion von Volumen \(V_A\) auf \(V_B\) erfolgt mit konstanter Temperatur \(T_H\). Da sich die Innere Energie bei einem isothermen Prozess nicht ändert, wird die aus dem heißeren Wärmebecken aufgenommene Wärme \(Q_1\) direkt als Arbeit \(W_1\) an den Kolben weitergegeben.
\[ Q_1 = W_1 \]
2. Takt: Reversible adiabatische Expansion: Die Expansion von Volumen \(V_B\) auf \(V_C\) erfolgt ohne Wärmeaustausch mit der Umgebung. Die Temperatur des Gases sinkt von \(T_H\) auf \(T_K\) und der Druck sinkt von \(p_B\) auf \(p_C\). Da kein Wärmeaustausch stattfindet, stammt die gesamte Kolbenarbeit \(W_2\) aus einem Teil der Inneren Energie des Gases.
\[ \Delta U_2 = W_2 \]
3. Takt: Reversible isotherme Kompression: Die Kompression von Volumen \(V_C\) auf \(V_D\) erfolgt mit konstanter Temperatur \(T_K\). Da sich die Innere Energie bei einem isothermen Prozess nicht verändert, wird die aufgebrachte Arbeit \(W_3\) direkt an das Wärmebecken in Form von Wärme \(Q_3\) abgegeben.
\[ Q_3 = W_3 \]
4. Takt: Reversible adiabatische Kompression: Die Kompression von Volumen \(V_D\) auf \(V_A\) erfolgt ohne Wärmeaustausch mit der Umgebung. Die Temperatur des Gases steigt von \(T_K\) auf \(T_H\) und der Druck erhöht sich von \(p_D\) auf \(p_A\). Da kein Wärmeaustausch stattfindet, wird die gesamte aufgebrachte Arbeit \(W_4\) in die Erhöhung der Inneren Energie gesteckt.
\[ \Delta U_4 = W_4 \]
Das Gas befindet sich jetzt im selben thermischen Zustand (A) wie zu Beginn des 1. Takts und kann einen weiteren Zyklus durchlaufen.
14.13.9 Wirkungsgrad Carnot Kreisprozess
Mithilfe der Integralrechnung lässt sich der Wirkungsgrad eines Carnot-Kreisprozesses berechnen. Er lautet
\[ \eta_{c} = \frac{T_{H}-T_{K}}{T_{H}} = 1 - \frac{T_{K}}{T_{H}} \]
und ist identisch mit dem Wirkungsgrad, den wir beim Stirling-Kreisprozess hergeleitet haben. Der maximale Wirkungsgrad eines Kreisprozesses hängt also nicht von der Konstruktion der Maschine ab, sondern ausschließlich von den Temperaturen des heißen und des kalten Wärmebeckens.
Da der ideale Carnot-Kreisprozess reversibel ist, kann er in umgekehrter Richtung als Wärmepumpe verwendet werden. Die Leistungszahl \(\epsilon_{\text{c}}\) eines umgekehrt ablaufenden Carnot-Kreisprozesses lautet daher:
\[ \epsilon_{\text{c}} = \frac{1}{\eta_{c}} = \frac{T_{H}}{T_{H}-T_{K}} \]
