15.9 Strömungen mit innerer Reibung
Das Bild 15.76 zeigt die ungewöhnliche Bahn eines rotierenden Körpers. Dieses Foto entstand während der Vorbereitungen für den International Young Physicists’ Tournament (IYPT), einem internationalen Physik-Wettbewerb für Schülerinnen und Schülern.
Einige Effekte wie zum Beispiel den Bernoulli-Effekt können wir schon mit reibungsfreien Fluiden erklären. Andere Phänomene, wie zum Beispiel die Bahn des rotierenden Körpers in Bild 15.76, lassen sich damit nicht erklären. In diesem Kapitel werden wir uns wieder mit waagrecht strömenden Fluiden (Flüssigkeiten und Gase) beschäftigen, lassen aber Reibung zu.
15.9.1 Laminare Strömung und die Grenzschicht
Intermolekulare Kräfte (Van-der-Waals-Kräfte) wirken sowohl zwischen den Fluid-Teilchen als auch zwischen Fluid-Teilchen und der Oberfläche von Körpern. Um jeden angeströmten Körper bildet sich daher eine sogenannte Grenzschicht (engl. boundary layer) aus (Bild 15.77). Dabei ist die Strömungsgeschwindigkeit direkt an der Oberfläche null. Mit zunehmender Entfernung von der Oberfläche nimmt die Strömungsgeschwindigkeit zu, bis die ungestörte Strömungsgeschwindigkeit erreicht ist. Ab dieser Entfernung – also außerhalb der Grenzschicht (Bereich b) – hat der Körper keinen Einfluss mehr auf die Strömungsgeschwindigkeit (Bereich c).
In der Grenzschicht kommt es zur Ausbildung von geschichteten Bereichen stationärer Strömungen mit abnehmender Geschwindigkeit. Diese stationäre Strömung wird als laminare Strömung (engl. laminar flow) (von lateinisch lamina für Schicht) bezeichnet.
15.9.2 Turbulente Strömungen
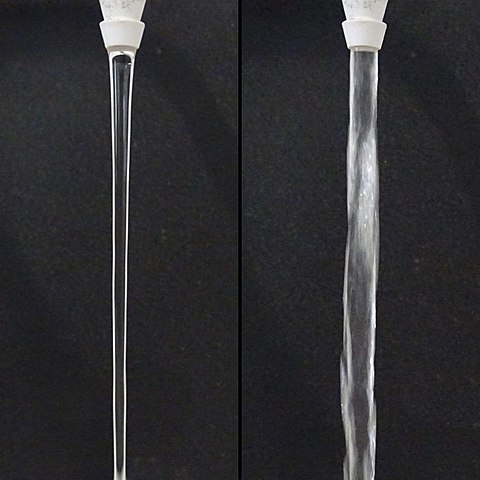
Durch intermolekulare Kräfte kommt es nicht nur zur Ausbildung zu einer Grenzschicht. Ab einer gewissen Strömungsgeschwindigkeit geht jede laminare Strömung in eine turbulente Strömung (engl. unsteady flow) über (Bild 15.78).
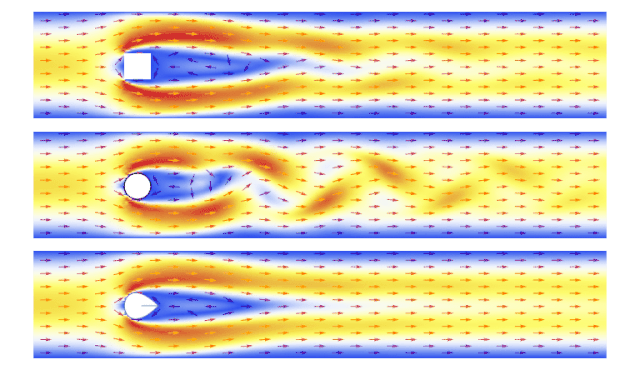
Wann es zum Übergang zu einer turbulenten Strömung kommt, hängt neben der Strömungsgeschwindigkeit auch von der Form des angeströmten Körpers ab (Bild 15.79).
In einer turbulenten Strömung ändert sich die Strömungsgeschwindigkeit (Größe und Richtung) an einem Punkt ständig. Deshalb kann eine turbulente Strömung nicht mehr durch ein einziges stationäres Stromlinienbild dargestellt werden.
15.9.3 Anhaften und Ablösen der Grenzschicht
Die intermolekularen Kräfte sind auch dafür verantwortlich, dass die Fluid-Teilchen der Oberfläche eines Körpers auch in dessen geometrischen Schatten folgen. In Bild 15.80 siehst du einen Wasserstrahl, der der Oberfläche eines Tischtennisballs (links) und eines Löffels (rechts) folgt (Anhaften der Grenzschicht).
Bei dem Ablösen der Grenzschicht löst sich die laminare Strömung hinter einem Körper in eine turbulente Strömung auf.
15.9.4 Verwirbelung
Anders als bei reibungsfreien Fluiden, kann es bei Strömung mit Reibung an der Grenze von Körpern zur Ausbildung von Wirbeln (engl. vortex) kommen, bei der die Fluid-Teilchen – abweichend von der Bewegungsrichtung des Körpers – schleifenförmige Bahnen beschreiben.
In Bild 15.81 siehst du ein weiteres Beispiel einer Verwirbelung. Die sogenannte Kármánsche Wirbelstraße entsteht, wenn sich hinter einem umströmten Körper gegenläufige Wirbel ausbilden. Du kannst sie manchmal im Wasser oder bei Wolken beobachten.
15.9.5 Strömungswiderstandskraft
Strömungswiderstandkraft (engl. drag) tritt auf, wenn die Bewegung eines Körpers durch ein ihn umgebendes Fluid behindert wird. Für die Größe des Strömungswiderstands sind im Wesentlichen zwei Faktoren entscheidend:
die Viskosität (Zähigkeit) des Fluids und die damit verbundene Reibung
die Form des angeströmten Körpers und die damit verbundene Wirbelbildung
Im Bild 15.82 siehst du, dass bei der angeströmten Kugel, die Fluid-Teilchen der Form nicht mehr folgen können und sich die Strömung von dem Körper ablöst. Die Änderung des Drehimpulses bei der Bildung der Wirbel erfordert Kraft. Generell gilt: Je mehr (und größere) Wirbel bei einer Bewegung entstehen, desto größer ist der Strömungswiderstand! Daher sollten Verkehrsmittel (zum Beispiel Autos oder Flugzeuge) möglichst „stromlinienförmig“ gebaut sein, um Treibstoff zu sparen.
Je geringer die Wirbelbildung bei einem angeströmten Körper ist, desto größer wird der Anteil der Reibung an der Grenzfläche zwischen Körper und Fluid an Strömungswiderstandskraft.
15.9.6 Newton-Reibung
Die allgemeine Beschreibung der Strömungswiderstandskraft ist mathematisch sehr kompliziert. Für den häufig vorkommenden Fall eines Körpers, der sich mit einer großen Geschwindigkeit durch ein Strömungsmedium mit einer kleinen Dichte (Gas) bewegt, gibt es eine Näherungsformel. In diesem Fall ist der Strömungswiderstand ungefähr proportional zur zweiten Potenz der Geschwindigkeit (\(F\stackrel{\propto}{\sim} v^2\)).
Der Betrag der Reibungskraft für diese Näherung (Newton-Reibung, engl. Newton drag) lautet:
| \[\begin{equation} F_\text{R} = \frac{1}{2}\cdot c_\text{w}\cdot A\cdot \rho\cdot v^2 \tag{15.11} \end{equation}\] |
In dieser Formel bedeuten:
- \(F_\text{R}\), der Strömungswiderstand (in \(\mathrm{N}\))
- \(c_\text{w}\), der Luftwiderstandsbeiwert (15.9.7, dimensionslose Zahl)
- \(A\), die angeströmte Querschnittsfläche (in \(\mathrm{m^2}\)) senkrecht zur Bewegungsrichtung
- \(\rho\), die Dichte des Fluids (in \(\mathrm{kg/m^3}\))
- \(v\), die Geschwindigkeit zwischen Körper und Fluid (in \(\mathrm{m/s}\))
Zum Beispiel kannst du diese Formel für Berechnung des Luftwiderstands eines schnell fahrenden Autos oder für einen Körper im freien Fall mit Luftwiderstand verwenden.
15.9.7 Luftwiderstandsbeiwert
Der Luftwiderstandsbeiwert (engl. drag coefficient) oder \(c_\mathrm{w}\)-Wert ist eine dimensionslose Größe (Zahl) für den Strömungswiderstand eines umströmten Körpers. Je kleiner die Zahl, desto „windschlüpfiger“ der Körper.
Der Luftwiderstandsbeiwert kann im Windkanal ermittelt werden. Im angeströmten Zustand wird die Strömungswiderstandskraft \(F_w\) (in \(\mathrm{N}\)) und der Staudruck \(p_\mathrm{stau}\) (in \(\mathrm{Pa}\)) gemessen. Mit der Formel
| \[\begin{equation} c_{\mathrm {w} } = {\frac {F_{\mathrm {w} }}{p_\mathrm{stau} \cdot A}} \tag{15.12} \end{equation}\] |
kann der Luftwiderstandsbeiwert berechnet werden. Die Fläche \(A\) (in \(\mathrm{m}^2\)) ist dabei die angeströmte Stirnfläche des Fahrzeugs. Der kleinstmögliche \(c_w\)-Wert ist null.
Bild 15.83: Der Rumpler-Tropfenwagen (Technikmuseum Berlin)
Der Rumpler-Tropfenwagen (Bild 15.83) wurde um 1920 gebaut und hat einen tropfenförmigen Grundriss. Sein Luftwiderstandsbeiwert beträgt nur \(0{,}28\) – das entspricht ungefähr dem \(c_\mathrm{w}\)-Wert eines modernen Pkws. Eine innen angeströmte hohle Halbkugel (Fallschirm ohne Loch) ist extrem strömungsungünstig. Hier beträgt der \(c_\mathrm{w}\)-Wert \(1{,}33\). Werte für gängige Körperformen findest du in Nachschlagewerken, wie zum Beispiel in der Wikipedia.
Da
\[ [c_{\mathrm {w} }] = {\frac {[F_{\mathrm {w}] }}{[p_\mathrm{stau}] \cdot [A]}} = {\frac {\cancel{\mathrm{N}}}{\frac{\cancel{\mathrm{N}}}{\cancel{\mathrm{m^2}}} \cdot \cancel{\mathrm{m^2}}}} \]
kürzen sich alle Einheiten und der Luftwiderstandsbeiwert ist somit eine dimensionslose Zahl.
15.9.8 Wirbelgröße
Rotationsenergie und Drehimpuls wachsen mit dem Quadrat des Radius. Daraus folgt, dass viele kleine Wirbel einen kleineren Strömungswiderstand verursachen als wenige große Wirbel.
Eine Verkleinerung der Wirbelgröße wird durch Aufrauen der Oberfläche erreicht. Beispiele dafür sind die Dellen auf der Oberfläche von Golfbällen oder die Struktur der Haut von Haien („Riblets“, Bild 15.84). Moderne Flugzeuge wie zum Beispiel der Airbus 380 besitzen eine Oberfläche nach dem gleichen Prinzip. Dabei kann rund \(1{,}5\,\%\) des Treibstoffs eingespart werden.
Links:
15.9.9 Magnus-Effekt
Dreht sich ein runder Körper beim Durchströmen eines Fluids, bewirkt das Anhaften der Grenzschicht eine Richtungsänderung (und damit eine Impulsänderung) der Fluid-Teilchen. Nach der Impulserhaltung muss der Gesamtimpuls erhalten bleiben. Die Ablenkung bewirkt also eine Impulsänderung des Körpers in die entgegengesetzte Richtung – hier eine Ablenkung nach unten (Bild 15.85). Dieses Phänomen wird nach Heinrich Gustav Magnus Magnus-Effekt (engl. Magnus effect) genannt.
.jpg){kind=link}
Der Magnus-Effekt spielt eine sehr wichtige Rolle im Ballsport, wo der Effet des Balles dem Spieler eine gezielte Richtungsänderung gestattet (Stichwort: Bananenflanke). Beim Flettner-Rotor wird dieser Effekt sogar als Antrieb von Schiffen verwendet.
