C.3 Simulation mit Python
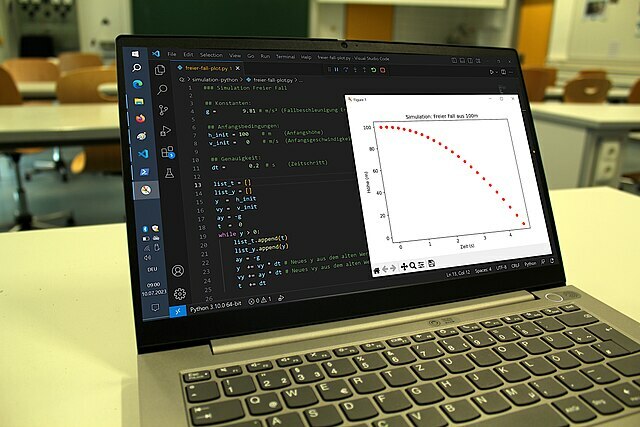
In diesem Kapitel zeigen wir dir, wie du Physiksimulationen mit der Programmiersprache Python durchführen kannst (Bild C.17).
Python gilt als einfache und leicht zu erlernende Programmiersprache und ist auch unter Profis sehr beliebt. Arbeitest du auf einem Linux-Betriebssystem, ist Python schon auf deinem System vorhanden. Verwendest du ein anderes Betriebssystem, musst du Python möglicherweise erst auf deinem Computer installieren. Im Internet findest du auch Dienste, die es dir gestatten, Python-Programme direkt im Browser zu schreiben und auszuführen.
C.3.1 Voraussetzungen
In diesem Kapitel findest du keine Einführung in die Programmiersprache Python. Zu diesem Thema gibt es viele Bücher für jede Altersgruppe. Wenn dich dieses Thema interessiert, besorge dir ein passendes Buch aus der öffentlichen Bibliothek oder suche im Internet nach Anleitungen.
Im Folgenden gehen wir davon aus, dass:
- Die Programmiersprache Python auf deinem System installiert ist.
- Du weißt, wie du in einem Texteditor das Programm
print("Hello Python!")schreibst. - Du weißt, wie du das Programm unter dem Namen
hello.pyspeicherst. - Du weißt, wie du eine Programmdatei
hello.pymit dem Python-Interpreter erfolgreich ausführst und den Text Hello, Python! als Ausgabe erhältst.
Links:
- Website: Erste Schritte mit Python
C.3.2 Konstanten und Startwerte festlegen
Als erste Aufgabe simulieren wir einen freien Fall ohne Luftwiderstand. Zunächst erstellen wir eine neue Datei mit dem Namen sim-free-fall.py und speichern sie in einem Verzeichnis am Computer ab. Am Anfang des Programms legen wir die Konstanten und Startwerte als Variablen fest:
# Simulation Freier Fall
## Konstanten:
g = 9.81 # m/s² (Fallbeschleunigung Erde)
## Anfangsbedingungen:
s_0 = 100 # m (Anfangshöhe)
v_0 = 0 # m/s (Anfangsgeschwindigkeit)
## Genauigkeit:
dt = 0.2 # s (Zeitschritt)Bemerkungen:
Das
#-Zeichen leitet einen Kommentar ein. Alle Zeichen, die danach folgen, werden nicht als Programm ausgeführt, sondern dienen nur als Information für Personen, die den Quelltext lesen.Im Kommentar nach einer Zahl solltest du immer die Einheit angeben, damit es später zu keinen Verwechslungen kommt.
Komma-Zahlen werden mit einem Punkt geschrieben (und nicht mit einem Beistrich)!
Untersuchst du später andere Fälle (größere Fallhöhe, Fallbeschleunigung am Mond,…) brauchst du nur in diesem Teil des Programms Werte zu ändern. Die eigentliche Schleife (siehe nächster Abschnitt) bleibt unverändert.
C.3.3 Schleife definieren
Für das wiederholte Berechnen der Werte mithilfe der Formeln für Bewegungssimulationen benötigen wir eine Schleife. Zu Beginn erhalten alle Variablen ihre Anfangswerte (s vertikaler Ort, v vertikale Geschwindigkeit, a vertikale Beschleunigung und t die Zeit).
## Simulation:
a = -g
s = s_0
v = v_0
t = 0
while s > 0:
s += v * dt # neues s aus dem alten Wert von v berechnen
v += a * dt # neues v aus dem alten Wert von a berechnen
t += dtDie Anweisungen innerhalb der while-Schleife werden so lange wiederholt, bis die angegebene Bedingung ungültig geworden ist (in unserem Fall: s kleiner oder gleich null geworden ist). Die Anweisungen berechnen die aktuellen Werte der Variablen aus denen des vorherigen Zeitschritts. Das Gleichheitszeichen (=) bedeutet keine Gleichheit im mathematischen Sinn, sondern eine Zuweisung. Der Ausdruck t = t + dt bedeutet also, dass zum aktuellen Wert von t der Wert von dt addiert und anschließend das Ergebnis der Rechnung in der Variable t gespeichert wird.
Vorsicht: Im Gegensatz zu vielen anderen Programmiersprachen spielt die Einrückung am Beginn der Zeile in Python eine entscheidende Rolle. Sie zeigt dem Computer an, wo der Schleifenblock endet.
Links:
- Website: A Byte of Python: Einrückung
- Website: A Byte of Python: Die while-Anweisung
C.3.4 Ausgabe
Als einfachste Auswertung kannst du die Werte nach dem Ende der Simulation als Textausgabe anzeigen lassen:
## Textausgabe:
print("Falldauer: ", round(t,3), " s")
print("Endgeschwindigkeit: ", round(v,3), "m/s")Der round(...) Befehl rundet einen Wert auf die angegebene Anzahl an Stellen (hier: 3 Stellen).
Speicherst du das Programm und führst es aus, erhältst du die Ausgabe:
Falldauer: 4.8 s
Endgeschwindigkeit: -47.088 m/sFür diese einfache Bewegung hätten wir gar keine Simulation benötigt. Das Anwendungsbeispiel zur Fallbewegung zeigt dir, wie du die exakten Werte berechnen kannst. Sie lauten für den Fall aus einer Höhe von \(100\;\mathrm{m}\): \(4{,}51\ldots\;\mathrm{s}\) und \(44{,}29\ldots\;\mathrm{m/s}\).
Links:
- Programm:
sim-free-fall.py
C.3.5 Grafische Ausgabe
Python stellt lediglich die Grundfunktionalität einer Programmiersprache zur Verfügung. Für die unterschiedlichsten Verwendungszwecke gibt es aber eine große Anzahl an Paketen, die diese Grundfunktionalität erweitern. Für die graphische Ausgabe von Diagrammen verwenden wir das Paket matplotlib. Damit wir das Paket im Programm importieren und verwenden können, muss das Paket zuerst auf den Computer heruntergeladen werden. Diese Aufgabe übernimmt der Python-Paketmanager pip. Der Aufruf lautet: pip install matplotlib.
Wir werden das bestehende Programm nun so erweitern, dass wir alle Schritte der Simulation als Graph ausgeben. Dazu speichern wir das Programm zunächst unter einem anderen Namen ab („speichern unter“) sim-free-fall-plot.py, damit das Originalprogramm unverändert bleibt.
Wir „merken“ uns die zu zeichnenden Werte in sogenannten Listen. Auf diese Weise können wir nach der Simulation alle Werte auf einmal zeichnen. Wir erweitern die Schleife wie folgt:
## Simulation:
list_t = []
list_s = []
a = -g
s = s_0
v = v_0
t = 0
while s > 0:
list_t.append(t)
list_s.append(s)
s += v * dt # neues s aus dem alten Wert von v berechnen
v += a * dt # neues v aus dem alten Wert von a berechnen
t += dtDie Zeile list_t = [] erzeugt eine neue leere Liste mit dem Namen list_t zum „Merken“ der Zeitwerte. Die Anweisung list_t.append(t) in der Schleife fügt den aktuellen Wert von t am Ende der Liste hinzu. Dasselbe machen wir mit den Ortswerten in der Liste list_s = [].
Für das Diagramm benötigen wir die Funktionen des Pakets matplotlib. Damit Python diese kennt, müssen wir sie zuerst mit der Anweisung import laden.
## Diagramm:
import matplotlib.pyplot as plt
plt.plot(list_t, list_s, 'ro')
plt.ylabel('Höhe (m)')
plt.xlabel('Zeit (s)')
plt.title('Simulation: Freier Fall aus '+str(s_0)+'m')
plt.show()Bemerkungen:
'ro'im Plot-Befehl ist eine Kurznotation für „rote Kreise“.- Anders als bei
print(...)müssen wir hier zunächst alle Zahlen in Text umwandeln. Das erledigt der Befehlstr(...). - Mit dem
+Operator werden mehrere Texte zu einem Text zusammengefasst. importAnweisungen können wie hier einfach vor der ersten Verwendung im Quelltext stehen. Es ist aber üblich, dass alle import-Anweisungen im Kopf der Quelltext-Datei geschrieben werden – noch vor dem eigentlichen Programm.
Führst du das Programm aus, öffnet der show()-Befehl ein separates Fenster mit dem Diagramm in Bild C.18. Klickst du in diesem Fenster auf das Disketten-Symbol, kannst du das Diagramm in verschiedenen Bildformaten speichern.
Links:
- Website: pip documentation - Getting Started
- Programm:
sim-free-fall-plot.py
C.3.6 Bocksprung-Verfahren
Das Bocksprung-Verfahren hast du schon kennengelernt. Es ist eine Methode, um genauere Ergebnisse bei einer Simulation zu erhalten. Dabei werden Ort und Geschwindigkeit um einen halben Zeitschritt versetzt berechnet.
In unserem Programm für den freien Fall ohne Luftwiderstand ändert sich nur der anfängliche Wert für die Geschwindigkeit (Zeile 16). Die Berechnungen aller anderen Werte bleiben gleich:
## Simulation:
a = -g
s = s_0
v = v_0 + a * dt/2 # wir beginnen mit der Geschwindigkeit v_½dt
t = 0
while s > 0:
s += v * dt # neues s aus dem alten Wert von v berechnen
v += a * dt # neues v aus dem alten Wert von a berechnen
t += dtDie Textausgabe der Endwerte für die Simulation mit dem Bocksprung-Verfahren lautet:
Falldauer: 4.6 s
Endgeschwindigkeit: -46.107 m/sDiese Ergebnisse liegen tatsächlich näher an den exakten Lösungen (\(t=4{,}51\ldots\;\mathrm{s}\) und \(v=44{,}29\ldots\;\mathrm{m/s}\)) als beim Euler-Verfahren.
C.3.7 Veränderliche Kraft
Körper fallen auf der Erdoberfläche im Allgemeinen nicht mit derselben Beschleunigung. Grund dafür ist der Luftwiderstand in der Atmosphäre. Als Beispiel für eine Simulation mit veränderlicher Kraft simulieren wir mit einem Python-Programm das Verhalten eines fallenden Körpers mit Luftwiderstand. Als Körper nehmen wir eine homogene Kugel mit dem Radius \(r=0{,}1\;\mathrm{m}\) (\(10\;\mathrm{cm}\)). Betrachten wir eine „Styropor“-Kugel (Expandiertes Polystyrol, EPS) finden wir in den Datenblättern eine Dichte von rund \(\rho=20\;\mathrm{kg/m^3}\) und damit eine Masse von \(m=0{,}083\ldots\;\mathrm{kg}\). Die Strömungswiderstandskraft ist abhängig von:
- Luftwiderstandsbeiwert (für eine Kugel findest du in der Literatur den Wert \(c_\mathrm{w}=0{,}45\))
- angeströmte Querschnittsfläche (hier eine Kreisfläche mit \(A=2\pi\cdot r^2=0{,}031\ldots\;\mathrm{m^2}\))
- Dichte der Luft (rund \(\rho_0=1{,}29\;\mathrm{kg/m^3}\) unter Normalbedingungen)
- der momentanen Geschwindigkeit des Körpers durch die Luft
Diese zusätzlichen Parameter werden im Kopf eingetragen:
# Simulation: Freier Fall einer Styroporkugel (r = 10cm; ρ = 20kg/m³) mit Luftwiderstand
## Konstanten:
g = 9.81 # m/s² (Fallbeschleunigung Erde)
m = 0.08 # kg (Masse des Körpers)
c_w = 0.45 # (Luftwiderstandsbeiwert)
A = 0.03 # m² (Fläche des Körpers normal zur Bewegungsrichtung)
rho = 1.29 # kg/m³ (Dichte des Mediums)
## Anfangsbedingungen:
s_0 = 100 # m (Anfangshöhe)
v_0 = 0 # m/s (Anfangsgeschwindigkeit)
## Genauigkeit:
dt = 0.2 # s (Zeitschritt)Im Gegensatz zur Simulation zum freien Fall ohne Luftwiderstand ist die Beschleunigung jetzt nicht mehr konstant und muss in jedem Zeitschritt aus der Kraft neu berechnet werden.
- Die Gesamtkraft ist hier die Summe aus Gewichtskraft \(F_\text{G} = -m\cdot g\) und Strömungswiderstandskraft \(F_\text{R}=-\frac{1}{2}\cdot c_\text{w}\cdot A\cdot \rho\cdot |v|\cdot v\) ergibt die aktuelle Kraft (
F = (-m*g) + (-0.5*c_w*A*rho*abs(v)*v)in Zeile 26) - Die aktuelle Beschleunigung berechnest du aus dem Quotienten aus der aktuellen Kraft und der Masse (\(F/m\), also
a = F/min Zeile 27)
Im Programm sieht das dann so aus:
## Simulation:
list_t = []
list_s = []
s = s_0
v = v_0
t = 0
while s > 0:
list_t.append(t)
list_s.append(s)
F = (-m*g) + (-0.5*c_w*A*rho*abs(v)*v)
a = F/m
s += v * dt # Neues s aus dem alten Wert von v berechnen.
v += a * dt # Neues v aus dem alten Wert von a berechnen.
t += dtIm Ort-Zeit-Diagramm (Bild C.19) der fertigen Simulation kannst du erkennen, dass die Kurve schon nach kurzer Fallzeit gerade verläuft – der Körper sich dort gleichförmig mit konstanter Geschwindigkeit (seiner Endgeschwindigkeit, engl. terminal velocity) bewegt. Gewichtskraft und Strömungswiderstandskraft sind dann entgegengesetzt gleich groß und heben einander auf.
Wiederholst du die Simulation mit einer gleich großen Kugel aus Eisen (\(m=32{,}98\ldots\;\mathrm{kg}\)), kannst du erkennen, dass die Kugel den Boden erreicht, bevor sie die Endgeschwindigkeit erreichen kann.
Links: