16.4 Relativistische Phänomene und Paradoxa
Kannst du dir vorstellen, einen \(10\;\mathrm{m}\) langen Stab in einer nur \(6\;\mathrm{m}\) langen Scheune unterzubringen (Bild 16.29)?
Die Eigenschaften der Natur, die uns die Relativitätstheorie zeigt, sind so jenseits unserer Alltagserfahrung, dass viele Leute auch heute noch die Relativitätstheorie infrage stellen. Es nützt aber nichts: Alle Experimente, die bis heute gemacht wurden, bestätigen ausnahmslos die Relativitätstheorie! Zu der Zeit, als Albert Einstein seine spezielle Relativitätstheorie veröffentlichte, konnten noch keine Experimente mit so großer Messgenauigkeit durchgeführt werden. Daher gab es viele Gedankenexperimente, die logische Widersprüche in seiner Theorie aufzeigen sollten.
In diesem Kapitel wirst du einige dieser klassischen Gedankenexperimente und noch das eine oder andere interessante relativistische Phänomen kennenlernen.
Links:
- Spiel: A Slower Speed of Light
16.4.1 Stab-Scheune-Paradoxon
Die Vorhersagen der Relativitätstheorie scheinen oft seltsam und auf den ersten Blick widersprüchlich. Das folgende Stab-Scheune-Paradoxon (engl. pole and barn paradox) Gedankenexperiment zeigt dir, dass die Relativitätstheorie konsistent (widerspruchsfrei) ist, wenn sie konsequent angewendet wird!
Eine Studentin der Physik hat eine geniale Idee, wie sie eine \(10\;\mathrm{m}\) lange Stange in eine \(6\;\mathrm{m}\) lange Scheune bringt. Wird der Stab auf eine Geschwindigkeit von \(80\,\%\) der Lichtgeschwindigkeit gebracht, verkürzt sich seine Länge aufgrund der Lorentzkontraktion auf \(6\;\mathrm{m}\) (Bild 16.30).
Um zu beweisen, dass der Stab tatsächlich – wenn auch nur für einen Augenblick – zur Gänze in der Scheune war, schließt sie gleichzeitig die Hintertür und öffnet die Vordertür.
Wie sieht ein Beobachter die Situation, der auf der Stange sitzt? Für ihn ist der Stab natürlich die ganze Zeit über \(10\;\mathrm{m}\) lang. Die Scheune bewegt sich mit \(80\,\%\) der Lichtgeschwindigkeit auf ihn zu und durch die Lorentzkontraktion schrumpft die Scheune auf \(3{,}6\;\mathrm{m}\) (Bild 16.31). Wie kann der Stab in dem einen Bezugssystem vollständig in der Scheune sein und in einem anderen nicht?
Trotzdem gibt es keinen Widerspruch: Der Beobachter auf dem Stab, sieht nämlich auch, dass die Türen nicht gleichzeitig geöffnet/geschlossen werden. Während die Vorderseite seines Stabes die Vordertür erreicht, öffnet sich diese. Zu einem späteren Zeitpunkt, wenn das Ende des Stabes in der Scheune verschwunden ist, schließt sich die Hintertür. Das Zeitintervall zwischen dem Öffnen der Vordertür und dem Schließen der Hintertür ist genauso groß, dass die restlichen \(6{,}4\;\mathrm{m}\) darin Platz finden.
16.4.2 Terrell-Rotation
Im Abschnitt über die Auswirkungen der endlichen Lichtlaufzeit auf das Beobachten haben wir bereits gesehen, wie sich die visuelle Wahrnehmung alleine durch „langsames Licht“ verändern würde. Außerdem hast du im Abschnitt über die Längenkontraktion erfahren, dass es zu einer Verkürzung aller Längen in Bewegungsrichtung bei relativ zu mir bewegten Körpern kommt. In Bild 16.32 siehst du nun beide Effekte im Vergleich dargestellt. Auf der linken Seite siehst du die gemessene Längenkontraktion. Auf der rechten Seite siehst du den visuellen Eindruck eines Beobachters, wenn die Längenkontraktion und die unterschiedlichen Lichtlaufzeiten der Würfelpunkte bis zum Auge berücksichtigt werden (Terrell-Rotation, engl. Terrell rotation).
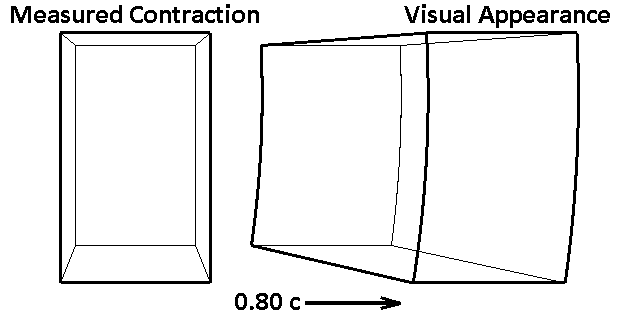
Bild 16.32: Verzerrung eines Würfels bei hohen Geschwindigkeiten (a) Längenkontraktion (b) Gesehen von einem Beobachter unter Berücksichtigung der Längenkontraktion und der endlichen Ausbreitungsgeschwindigkeit des Lichts
In Bild 16.33 siehst du den berechneten Vorbeiflug an einer Reihe von Würfeln mit hohen Geschwindigkeiten, bei dem beide Effekte – Längenkontraktion und endliche Lichtlaufzeit – berücksichtigt werden. Die Verzerrung der betrachteten ruhenden Würfel entsteht durch die perspektivische Abbildung, die unser Auge erzeugt.
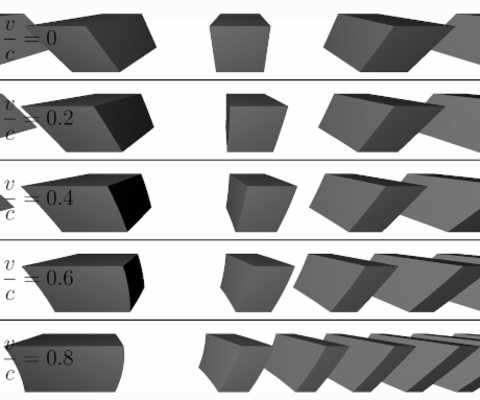
Bild 16.33: Vergleich des visuellen Eindrucks beim Vorbeiflug an einer Reihe von ruhenden Würfeln mit unterschiedlichen Geschwindigkeiten (Längenkontraktion und endliche Lichtlaufzeit).
Beachte, dass die Würfel, wenn sie sich mit hoher Geschwindigkeit annähern, in Bewegungsrichtung sogar verlängert erscheinen, obwohl sie durch die Längenkontraktion verkürzt sind! Ein wenig später sehen die Proportionen des Würfels – trotz Längenkontraktion – für uns korrekt aus, nur seltsam verdreht. Sehen wir den Würfeln hinterher, erkennen wir eine starke Verzerrung des Würfels in Bewegungsrichtung.
In diesem Abschnitt sind die Medien absichtlich unbunt. Denn ein Beobachter von färbigen Objekten sieht neben der Formänderung auch noch Farbänderung durch den relativistischen Dopplereffekt, den du im letzten Abschnitt kennengelernt hast.
Links:
- Spiel: A Slower Speed of Light
16.4.3 Zwillingsparadoxon
Stella verlässt als Teenager die Erde in einem Raumschiff, während ihre Zwillingsschwester Terra auf der Erde zurückbleibt. Das Raumschiff bewegt sich mit \(60\,\%\) der Lichtgeschwindigkeit (\(v=0{,}6\cdot c\), der Lorentzfaktor ist \(\gamma = 0{,}8\)). Auf der Erde vergehen 25 Jahre bis Stella wieder zurückkehrt. Terra misst, dass nach der Zeitdilatation an Bord von Stellas Raumschiff nur \(25\cdot 0{,}8=20\) Jahre vergangen sind. Bei der Rückkehr auf die Erde ist Stella \(25-20=5\) Jahre jünger als ihre Zwillingsschwester Terra (Bild 16.34).
Aus der Sicht von Stella hat sich aber die Zwillingsschwester auf der Erde mit \(60\,\%\) der Lichtgeschwindigkeit (\(v=0{,}6\cdot c\)) bewegt. Stella war \(20\) Jahre unterwegs. In dieser Zeit ist die Schwester auf der Erde aufgrund der Zeitdilatation \(20\cdot 0{,}8=16\) Jahre gealtert. Bei Stellas Rückkehr müsste sich also um \(20-16=4\) Jahre älter als Terra sein!
Treffen sich beide Zwillingsschwester am selben Ort, kann nicht beides der Fall sein. Dieser scheinbare Widerspruch wird Zwillingsparadoxon (engl. twin paradox) genannt.
Diese Überlegung hat aber einen Fehler. Die Gleichungen der speziellen Relativitätstheorie gelten nur für Inertialsysteme. Um zur Erde zurückzukommen, muss Stella irgendwann umkehren. Dabei kommt es unweigerlich zu einer Beschleunigung und ihr Bezugssystem ist kein Inertialsystem mehr – selbst eine Rundreise ist eine beschleunigte Bewegung. Die Beschreibung der Schwester auf der Erde ist daher die korrekte Version.
Aber wie stellt sich die Situation für die Schwester im Raumschiff dar? Auf der Hinreise, als auch auf der Rückreise (so lange sich ihr Raumschiff mit konstanter Reisegeschwindigkeit bewegt und es ein Inertialsystem bildet), altert die Schwester auf der Erde ja tatsächlich weniger als sie.
Um die Sache möglichst einfach zu machen, stellen wir uns ein zweites Raumschiff vor, das am Reiseziel zum selben Zeitpunkt vorbeikommt wie das Schiff der Schwester. Im Gegensatz zu ihrem Raumschiff bewegt es sich aber mit \(60\,\%\) der Lichtgeschwindigkeit Richtung Erde (\(v=-0{,}6\cdot c\)). Auf diese Weise muss kein Raumschiff abbremsen und die Schwester hüpft „einfach“ am Reiseziel von ihrem Raumschiff (Inertialsystem 1) zu dem zweiten Raumschiff (Inertialsystem 2), und kehrt so zur Erde zurück.
Bei diesem „fliegenden“ Wechsel der Raumschiffe passiert das Entscheidende: Durch den Wechsel des Inertialsystems ändert sich auch die Gleichzeitigkeit der Ereignisse. Unmittelbar vor dem Verlassen ihres Raumschiffs ist Stella \(10\) Jahre gealtert und Terra ist gleichzeitig \(8\) Jahre gealtert. Unmittelbar nach dem Wechsel des Bezugssystems ist Stella noch immer \(10\) Jahre gealtert, aber Terra gleichzeitig schon \(17\) Jahre gealtert. Das klingt sehr dramatisch, tatsächlich ändert sich durch den Bezugssystemwechsel aber nur der „Blickwinkel“ von Stella auf Terras Zeitachse. Auf der \(10\)-jährigen Rückreise altert Terra aus Sicht von Stella ebenfalls „nur“ \(8\) Jahre. Nach der Rückkehr ist Stella insgesamt jünger (\(2\cdot 10=20\) Jahre gealtert) als ihre Zwillingsschwester Terra (\(17+8=25\) Jahre gealtert).
Der abrupte Wechsel ist natürlich unrealistisch. Stell dir das Altern von Terra auf der Erde wie ein Video mit einer Gesamtspielzeit von \(25\) Jahren vor. Der Bordcomputer im Raumschiff übernimmt die Steuerung des Videos und zeigt Stella immer genau jene Stelle im Video, die aus ihrer Sicht gleichzeitig auf der Erde passiert. Zunächst würde Stella bei konstanter Reisegeschwindigkeit das Video ihrer Zwillingsschwester um die Zeitdilatation verlangsamt („slow motion“) sehen. Sobald die Abbrems- und Beschleunigungsphase am Reiseziel beginnt, steigt die Abspielgeschwindigkeit an und läuft sogar schneller als Normalgeschwindigkeit („fast forward“). Nähert sich das Raumschiff bei der Rückreise seiner konstanten Reisegeschwindigkeit, verlangsamt sich das Video, bis es wieder um die Zeitdilatation verlangsamt („slow motion“) abläuft. Wenn Stella nach \(20\) Jahren wieder auf der Erde ankommt, ist das Video gerade zu Ende.
Beachte: Für beide Schwestern vergeht die Zeit in ihrem eigenen Ruhesystem gleich schnell. Bei der Rückkehr auf die Erde ist Stella \(5\) Jahre jünger als ihre Zwillingsschwester, beide Schwestern haben aber die gleiche Lebenserwartung – das Reisen mit großer Geschwindigkeit verlängert also nicht die Lebenszeit.
16.4.4 Relativistischer Dopplereffekt
Bei den Wellen hast du bereits den akustischen Dopplereffekt kennengelernt. Im Gegensatz zu Schall hat Licht in allen Inertialsystemen aber dieselbe Ausbreitungsgeschwindigkeit. Daher müssen wir keine Fallunterscheidung treffen, ob sich die Quelle oder der Empfänger bewegen. Bezeichnet \(v\) die Relativgeschwindigkeit zwischen Quelle und Empfänger, lautet die Formel für den Relativistischen Dopplereffekt (engl. relativistic Doppler Effect):
| \[\begin{equation} f=f_0\cdot\sqrt {\frac {1+{\displaystyle\frac {v}{c}}}{1-{\displaystyle\frac {v}{c}}}} \tag{16.12} \end{equation}\] |
Da die Farbe des Lichts abhängig von der Wellenlänge ist, ändert sich die Farbe von leuchtenden Körpern, je nachdem, ob er sich annähert oder entfernt (Bild 16.35):
16.4.5 Herleitung des relativistischen Dopplereffekts
Beim akustischen Dopplereffekt haben wir die Fälle unterschieden, ob die Quelle ruht und sich der Empfänger bewegt oder sich die Quelle bewegt und der Empfänger ruht. Wir wenden jetzt die spezielle Relativitätstheorie auf beide Ausdrücke an. Für eine bessere Übersichtlichkeit verwenden wir in der Ableitung die in der relativistischen Physik übliche Abkürzung \(\beta = v/c\) mit der Relativgeschwindigkeit \(v\) zwischen Quelle und Empfänger:
- bewegte Quelle/ruhender Empfänger: „Bewegte Uhren gehen langsamer“ bedeutet hier, dass das Licht für den ruhenden Empfänger mit der um den Lorentzfaktor verkleinerten Frequenz „tickt“.
\[ \begin{aligned} f_B = {} & f_Q\cdot\sqrt {1-\beta^{2}}\cdot\left(\frac{1}{1-\beta}\right) \\ f_B = {} & f_Q\cdot\frac{\sqrt{1-\beta^{2}}}{1-\beta} &&\Bigr\rvert\; 0 < \beta \le 1 \Rightarrow x=\sqrt{x^2} \\ f_B = {} & f_Q\cdot\frac{\sqrt{1-\beta^{2}}}{\sqrt{(1-\beta)^2}} &&\Bigr\rvert\; 1=1^2 \\ f_B = {} & f_Q\cdot\sqrt{\frac{1^2-\beta^{2}}{(1-\beta)^2}} &&\Bigr\rvert\;\text{Binomische Formeln anwenden} \\ f_B = {} & f_Q\cdot\sqrt{\frac{\cancel{(1-\beta)}\cdot (1+\beta)}{\cancel{(1-\beta)}\cdot(1-\beta)}} \\ f_B = {} & f_Q\cdot\sqrt{\frac{1+\beta}{1-\beta}} &&\Bigr\rvert\; \beta=\frac{v}{c}\\ f_B = {} & f_Q\cdot\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}} \\ \end{aligned} \]
- ruhende Quelle/bewegter Empfänger: „Bewegte Uhren gehen langsamer“ bedeutet in diesem Fall, dass die Sekunde für den Empfänger länger dauert. Er erhält also pro Sekunde mehr Schwingungen und misst eine vergrößerte Frequenz. Setzen wir den Lorentzfaktor ein, erhalten wir:
\[ \begin{aligned} f_B = {} & f_Q\cdot\frac{1}{\sqrt{1-\beta^2}}\cdot\left(1+\beta\right) \\ f_B = {} & f_Q\cdot\frac{1+\beta}{\sqrt{1-\beta^2}} &&\Bigr\rvert\; 0 < \beta \le 1 \Rightarrow x=\sqrt{x^2} \\ f_B = {} & f_Q\cdot\frac{\sqrt{(1+\beta)^2}}{\sqrt{1-\beta^2}} &&\Bigr\rvert\; 1=1^2 \\ f_B = {} & f_Q\cdot\sqrt{\frac{(1+\beta)^2}{1^2-\beta^2}} &&\Bigr\rvert\;\text{Binomische Formeln anwenden} \\ f_B = {} & f_Q\cdot\sqrt{\frac{\cancel{(1-\beta)}\cdot (1+\beta)}{\cancel{(1-\beta)}\cdot(1-\beta)}} \\ f_B = {} & f_Q\cdot\sqrt{\frac{1+\beta}{1-\beta}} &&\Bigr\rvert\; \beta=\frac{v}{c}\\ f_B = {} & f_Q\cdot\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}} \\ \end{aligned} \]
Wie erwartet, liefern beide Fälle dieselbe Formel. Weil Licht kein Ausbreitungsmedium benötigt, spielt es bei der Frequenzänderung beim optischen Dopplereffekt keine Rolle, ob sich die Quelle oder der Empfänger bewegen, allein die Relativgeschwindigkeit zwischen beiden ist entscheidend.
16.4.6 Schneller als die Lichtgeschwindigkeit
Im Internet findest du gelegentlich Artikel und Videos, die behaupten, dass sich etwas schneller als mit Lichtgeschwindigkeit bewegt. Kann das stimmen?
Wir machen dazu folgendes Experiment: Im Freien zielst du mit dem Laserpointer in den Himmel. Dann kippst du dein Handgelenk in \(1\;\mathrm{s}\) um einen Winkel von \(90^\circ\), und zwar so, dass der Mond dabei überstrichen wird.
Die Bewegung entspricht einer Drehung mit einer Winkelgeschwindigkeit von
\[ \omega = \frac{\Delta\varphi}{\Delta t} =\frac{90^\circ}{1\;\mathrm{s}} =\frac{1{,}57\ldots\;\mathrm{rad}}{1\;\mathrm{s}} =1{,}57\ldots\;\mathrm{rad/s} \]
Der mittlere Abstand Erde-Mond beträgt rund 60 Erdradien, also \(60\cdot 6\,378\;\mathrm{km} = 382\,680\;\mathrm{km}\). In dieser Entfernung beträgt die Geschwindigkeit deines Lichtpunkts auf der Mondoberfläche (Tangentialgeschwindigkeit) rund
\[ v =r\cdot \omega =382\,680\,000\;\mathrm{m} \cdot 1{,}57\ldots\;\mathrm{rad/s} =601\,112\,338\;\mathrm{m/s} \]
Diese Geschwindigkeit entspricht rund der doppelten Vakuumlichtgeschwindigkeit von \(3\cdot 10^{8}\;\frac{\mathrm{m}}{\mathrm{s}}\)! Aber was passiert hier? Dein Lichtstrahl besteht aus vielen einzelnen Photonen, von denen sich keines schneller als mit Lichtgeschwindigkeit bewegt. Auch Schatten bewegen sich oft schneller als mit Lichtgeschwindigkeit. Du siehst: Dass sich „etwas“ mit Überlichtgeschwindigkeit bewegt, ist eigentlich keine große Kunst. Denn: Die Lichtgeschwindigkeit als Grenzgeschwindigkeit gilt nur für Materie, also einzelne Körper oder Teilchen!
16.4.7 Spezielle Relativitätstheorie und Elektromagnetismus
Bisher haben wir uns ausschließlich mit Bewegungslehre beschäftigt. Die Relativitätstheorie betrifft jedoch alle Bereiche der Physik. Albert Einsteins Arbeit zur speziellen Relativitätstheorie trägt sogar den Namen „Zur Elektrodynamik bewegter Körper“. In diesem Abschnitt möchten wir uns daher ein Beispiel aus dem Elektromagnetismus ansehen. Zuvor sei erwähnt, dass Ladung eine relativistisch invariante Größe ist. Die elektrische Ladung eines Elektrons zum Beispiel ist unabhängig von seiner Geschwindigkeit.
In Bild 16.37 siehst du eine Standardsituation aus dem Elektromagnetismus: Ein bewegtes Elektron erfährt in dem magnetischen Feld eines stromdurchflossenen Leiters eine anziehende Lorentzkraft. Der Leiter ist dabei elektrisch neutral (gleich viele positive wie negative Ladungsträger). Zur Vereinfachung wählen wir für die Geschwindigkeit der Ladung außerhalb des Leiters dieselbe Geschwindigkeit wie für die Leiterelektronen im Inneren.
In Bild 16.38 siehst du die Situation von vorhin aus der Sicht des ruhenden Elektrons. Hier bewegen sich die Elektronen nicht. Stattdessen bewegen sich die positiven Ladungen in die entgegengesetzte Richtung. Auch hier entsteht durch den Strom der positiven Ladungsträger ein Magnetfeld (nicht im Bild dargestellt). Die Kraft auf das Elektron kann dadurch allerdings nicht erklärt werden, denn ein Magnetfeld übt nur Kraft auf bewegte Ladungen aus.
Jetzt kommt die Relativitätstheorie ins Spiel: durch die Lorentzkontraktion der nun bewegten positiven Ladungen (Atomrümpfe) erhöht sich deren Dichte. Für die nun ruhenden Elektronen entfällt die Lorentzkontraktion. Ihre Dichte im Leiter nimmt entsprechend ab. Daher ist der Leiter in diesem Inertialsystem nicht mehr elektrisch neutral. Für die Kraft auf das Elektron ist jetzt ein elektrisches Feld verantwortlich.
So wie Raum und Zeit eine Einheit bilden, sind auch das elektrische und das magnetische Feld untrennbar miteinander verwoben. Sie sind ebenfalls keine absoluten Begriffe, sondern gehen – je nach gewähltem Inertialsystem – ineinander über.
Da die Driftgeschwindigkeit von Leiterelektronen nur im Bereich von hundertstel Millimeter pro Sekunde ist, wirst du dich vielleicht wundern, wie sich bei diesen niedrigen Geschwindigkeiten überhaupt relativistische Effekte bemerkbar machen können. Der Grund ist die hohe Dichte von Leiterelektronen (etwa \(10^{23}/\mathrm{cm^3}\)). Trotz eines Lorentzfaktors nahe eins, ergibt das in Summe eine beträchtliche Coulombkraft.









