5.8 Anwendungen der Impulserhaltung
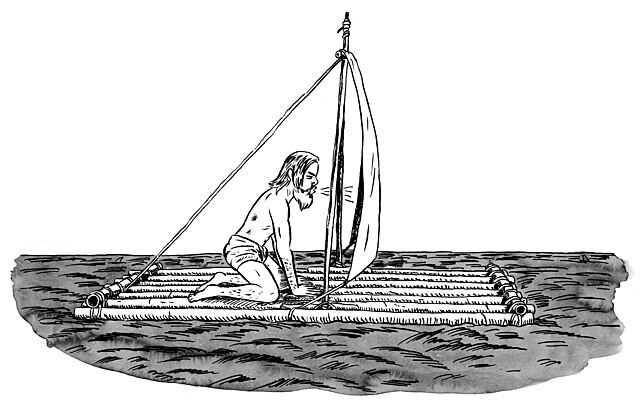
In das eigene Segel blasen um bei einer Flaut voran zu kommen. Kann das tatsächlich funktionieren.
In diesem Kapitel wenden wir den Impulserhaltungssatz auf einige wichtige und bekannte Systeme an und klären Sachverhalte, wie der oben angedeutete.
5.8.1 Rückstoßantrieb
In Bild 5.36 siehst du eine Person im All, die ein Werkzeug von sich schleudert, um sich in die Gegenrichtung zu bewegen. Sie nutzt dabei den Impulserhaltungssatz. Da sie relativ zum Schraubenschlüssel eine große Masse besitzt, fällt ihre Geschwindigkeitsänderung verhältnismäßig klein aus. In der Abwesenheit eines Düsenrucksacks oder einer Sicherheitsleine verbunden mit dem Raumschiff, ist das Abwerfen von Ausrüstungsgegenständen aber die einzige Möglichkeit im Weltall, seinen Bewegungszustand zu ändern!
Dieses Rückstoßprinzip (engl. jet propulsion) ist die Grundlage aller Antriebsarten zu Wasser, in der Luft und im Weltall. Hier einige Beispiele:
Dabei wird ein Treibmittel (engl. propellant) (etwa Wasser oder heißes Gas einer Verbrennung) einmalig (zum Beispiel bei einer Feuerwaffe) oder ständig (zum Beispiel bei einer Rakete) ausgeworfen, um einen Körper entgegen der Ausstoßrichtung zu beschleunigen.
Ein beliebtes Experiment zum Rückstoßprinzip ist die Wasserrakete (engl. water rocket) (Bild 5.37). Dabei wird eine PET-Flasche zum Teil mit Wasser gefüllt und über ein Ventil am Flaschenhals der Innendruck mit einer Fahrradluftpumpe erhöht (der Berstdruck von Einweg-PET-Flaschen liegt bei rund 8 bar, der von Mehrweg-PET-Flaschen sogar bei etwa 20 bar). Wird die Flasche so aufgestellt, dass die Öffnung nach unten zeigt und das Ventil geöffnet, sorgt die Druckluft im Kopf der Wasserrakete für den Ausstoß des Wassers. Das Verhältnis von Wasser- zu Luftvolumen ist entscheidend. Bei zu wenig Wasser verpufft der verbleibende Luftdruck, ohne Wasser zu beschleunigen. Andererseits ist bei zu wenig Luftvolumen die Luft entspannt, bevor das gesamte Wasser ausgestoßen wurde. Als Faustregel gilt das Verhältnis von 1:2 von Wasser zu Luft. Der aktuelle Weltrekord für eine mit Wasser und Luft betriebene Rakete liegt bei einer Steighöhe von unglaublichen 830 Metern!
Links:
5.8.2 Schubumkehr
Bläst du in dein eigenes Segel, um bei einer Flaute voranzukommen, scheint das ebenso sinnlos wie der Versuch, sich am eigenen Haarschopf aus dem Sumpf zu ziehen, wie in der Lügengeschichte von Baron Münchhausen. Während wir uns aufgrund des Wechselwirkungsgesetzes unmöglich an den eigenen Haaren selbst anheben können, funktioniert die Idee, in das eigene Segel zu blasen, prinzipiell schon.
Im Folgenden ersetzen wird das Pusten von Luft gedanklich durch ein Katapult mit einer Kugel (Bild 5.38, a). Da es zunächst keine Geschwindigkeiten gibt, muss der Gesamtimpuls des Systems zu Beginn null sein. Wir die Kugel abgeschossen, erhält sie einen Impuls \(p\). Aufgrund der Impulserhaltung muss der Gesamtimpuls wie zuvor null sein. Das Floß erfährt daher beim Abschuss den Gegenimpuls \(-p\). Trifft die Kugel auf das „Segel“ wird die Bewegung in der Gegenrichtung umgeleitet. Das entspricht einer Impulsänderung von \(\Delta p = (-p)-(p) = -2p\). Und auch das Floß erfährt dieselbe Impulsänderung in die Gegenrichtung (\(\Delta p = (p)-(-p) = 2p\)). Trägt die Kugel jetzt den Impuls \(-p\) fort, behält das Floß den Impuls \(p\) in die Vorwärtsrichtung bei.
In der Praxis scheitern wir einfach daran, dass wir nicht stark genug blasen können. Würden wir allerdings Wasser unter dem Boot mit einer Pumpe ansaugen und den Strahl auf das Segel richten (ähnlich einer Pelton-Turbine), könnten wir das Boot tatsächlich auf diese Weise antreiben.
Dieses Prinzip wird zum Beispiel bei der Schubumkehr (engl. thrust reversal) von Flugzeugen verwendet. Setzt die Maschine auf dem Boden auf, werden am Triebwerk kleine „Segel“ ausgeklappt, die den Strahl des Triebwerks gegen die Flugrichtung umleiten und so die Maschine abbremsen (Bild 5.39). Damit es während des Fluges zu keiner Schubumkehr kommt, gibt es einige clevere Sicherheitsvorkehrungen. Zum Beispiel kann sie nur dann ausgelöst werden, wenn mindestens eines der ausgefahrenen Räder belastet ist und zusätzlich die Flughöhe unter ein paar Metern liegt.
5.8.3 Ballistisches Pendel
Das ballistische Pendel ist ein einfaches mechanisches Gerät zur Bestimmung der Geschwindigkeit von Projektilen. Dabei wird ein Projektil der Masse \(m\) in ein, an Schnüren aufgehängtes, Holzstück der Masse \(M\) (das Pendel) geschossen und bleibt dort stecken, daher handelt es sich um einen vollkommen unelastischen Stoß (Bild 5.40).
Aus der Impulserhaltung folgt (Gesamtimpuls vorher gleich Gesamtimpuls nachher):
\[ m\cdot v = (M+m)\cdot v' \]
Nach dem Stoß besitzt das Holzstück mit dem Projektil die kinetische Energie:
\[ E_{\mathrm {KIN} }= {\frac {(M+m)\cdot v'^{2}}{2}} \]
Das Pendel schwingt zur Seite aus und die anfängliche kinetische Energie \(E_{\mathrm {KIN} }\) wandelt sich in potenzielle Energie \(E_{\mathrm {POT}}\) um.
\[ E_{\mathrm {POT}} = (M+m)\cdot g\cdot h \]
Am höchsten Punkt wird die Hubhöhe \(h\) des Holzstücks bestimmt. Daraus lässt sich jetzt ein Zusammenhang von Geschossgeschwindigkeit \(v\) und Hubhöhe des Pendels herleiten:
Gleichsetzen von \(E_{\mathrm {KIN}}\) und \(E_{\mathrm {POT}}\) Energie liefert:
\[ \frac{(M+m)\cdot v'^{2}}{2}= (M+m)\cdot g\cdot h \]
Wir formen die Gleichung so um, dass wir für die Geschwindigkeit nach dem Stoß den Ausdruck
\[ v'={\sqrt {2\cdot g\cdot h}} \]
erhalten. Als Letztes setzen wir \(v'\) in den Ausdruck für die Impulserhaltung ein:
\[ m\cdot v=(M+m)\cdot {\sqrt {2\cdot g\cdot h}} \]
Damit erhalten als Ausdruck für die ursprüngliche Geschossgeschwindigkeit
\[\begin{align} v = {} & {\frac {(M+m)\cdot {\sqrt {2\cdot g\cdot h}}}{m}} \notag \\ = {} & \left(1+{\frac {M}{m}}\right)\cdot {\sqrt {2\cdot g\cdot h}} \tag{5.17} \\ \end{align}\]
Sind die Massen von Holzstück und Projektil sowie die entstandene Hubhöhe bekannt, lässt sich die Geschwindigkeit des Projektils berechnen.
5.8.4 Swing-by Manöver
Ein eleganter Trick bei interplanetaren Raumflügen Treibstoff zu sparen, ist das Swing-by Manöver. Dabei wird eine Raumsonde so gesteuert, dass sie nahe bei einem Planeten vorbeifliegt. Je nachdem, wie die Bahn am Planeten vorbei geführt wird, kann die Raumsonde beschleunigt oder verlangsamt werden.
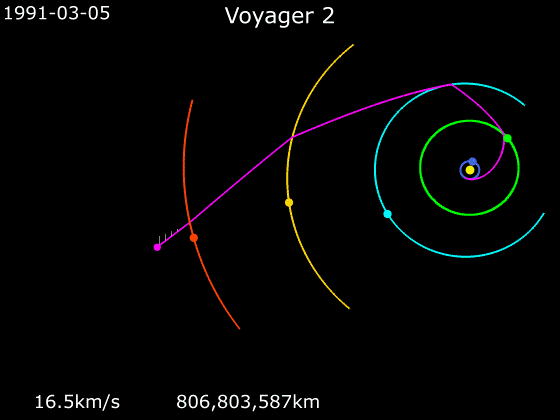
Bild 5.41: Swing-by Manöver von Voyager 2 bei ihrem Flug durch das Sonnensystem
Dieses Manöver kann als langsam ablaufender, elastischer Stoß betrachtet werden. Auch hier gilt die Energie- und Impulserhaltung. Die zusätzliche Bewegungsenergie und den zusätzlichen Impuls, den die Raumsonde nach dem Swing-by Manöver erhält, stammen von dem Planeten. Aufgrund der enormen Massenunterschiede von Raumsonde und Planet ist die Bewegungsänderung des Planeten unmessbar klein.
5.8.5 Entdeckung des Neutrinos
Bei einem Beta-Zerfall zerfällt ein Neutron in ein Proton und ein Elektron. Aus Experimenten war bekannt, dass bei diesem Prozess der Energie- und Impulserhaltungssatz nicht erfüllt sind. Sollte diese Erhaltungssätze nicht im subatomaren Bereich gelten?
Der Wissenschaftler und Nobelpreisträger Wolfgang Pauli war der Meinung, dass Energie- und Impulserhaltungssatz auch hier gelten, allerdings – so vermutete er – entsteht bei einem Beta-Zerfall ein weiteres Teilchen, das bisher unentdeckt geblieben ist und für den fehlenden Impuls und die fehlende Energie aufnimmt. Der Physiker italienische Enrico Fermi (Bild 5.42) gab dem hypothetischen Teilchen ein paar Jahre später den Namen Neutrino („kleines Neutron“).
Es hat noch über 20 Jahre gedauert, bis es den Physikerinnen und Physikern gelang, das Neutrino tatsächlich im Experiment (Projekt „Poltergeist“) nachzuweisen und die Theorie von Wolfgang Pauli zu bestätigen. Warum es noch so lange gedauert hat, liegt an den unglaublichen Eigenschaften von Neutrinos: Es reagiert kaum mit Materie. Die Sonne sendet ständig Neutrinos aus. Dein Körper wird pro Sekunde ungefähr von unglaublichen 400.000 Milliarden Neutrinos von der Sonne durchdrungen, aber in deinem ganzen Leben wechselwirkt nur ein einziges Neutrino mit deinem Körper.